L’optimisation combinatoire, une technologie mature au service de la performance


Cet article explore l’optimisation combinatoire, un domaine d’IA pour des décisions optimales dans des contextes complexes. Moins médiatisée que le machine learning, elle offre des applications matures. Le texte présente des méthodes comme la programmation linéaire, les heuristiques, avec un cas d’étude sur l’optimisation des achats.
L’optimisation combinatoire est un domaine de l’Intelligence Artificielle¹ qui vise principalement à aider à prendre les meilleures décisions dans un environnement complexe. Ayant atteint son plateau de productivité depuis quelques années, elle est considérée aujourd’hui moins hype que l’apprentissage automatique (Machine Learning) ou l’apprentissage profond (Deep Learning), mais elle l’était tout autant dans les années 1960-1970 avec des innovations algorithmiques comme la méthode du Simplex (1947) ou le Branch-and-Bound (1960), et la résolution du problème du voyageur de commerce sur 48 villes (1954).
Ces techniques ont permis par exemple aux compagnies pétrolières d’économiser des millions de dollars dans les années ‘60, et les implémentations commerciales de ces techniques ont été bien acceptées car facilement utilisables sur les ordinateurs disponibles à l’époque. Malgré quelques désillusions et difficultés de mise en production sur de grosses instances entre les années ‘90 et 2000, cette technologie est aujourd’hui mature et largement adoptée par de nombreux secteurs d’activité (e.g. supply chain, logistique, production et distribution énergétique, planification, ordonnancement, tournées de véhicules, etc.). La figure suivante illustre l’évolution de l’intérêt pour la technique d’optimisation en variables mixtes (avec variables entières et non entières) également appelée MIP.
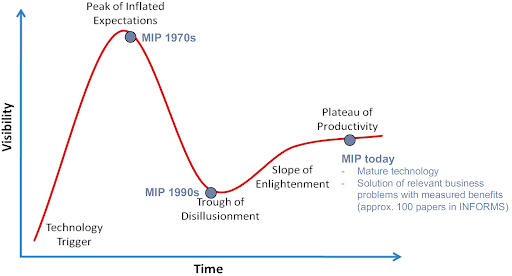
Les algorithmes d’Optimisation, Recherche Opérationnelle, ou tout simplement R.O., font appel à des techniques variées de modélisation tant sur le plan mathématique et informatique que pour la transcription d’une problématique métier. Tandis que les algorithmes d’apprentissage machine requièrent une quantité importante de données pour en extraire de la connaissance, la principale valeur ajoutée d’un algorithme en optimisation consiste à explorer efficacement l’espace des solutions pour résoudre un problème donné. Certains diraient que toutes ces approches sont complémentaires et c’est bien souvent le cas : par exemple, un modèle d’apprentissage automatique peut être employé pour prévoir les données d’une instance d’un problème d’optimisation combinatoire, ou à l’inverse une stratégie d’optimisation continue est incluse dans un réseau neuronal afin de minimiser sa fonction de coût. En particulier, l’apprentissage d’un réseau neuronal minimise sa fonction de coût usuellement selon une descente de gradient stochastique qui met à jour les paramètres du réseau par itération ; la méthode Adam présente l’avantage d’ajuster automatiquement la quantité mise à jour à chaque itération de cette descente.
Formellement, un algorithme d’optimisation vise à minimiser ou maximiser une fonction objectif sous certaines contraintes, et une telle approche est généralement opportune lorsque se présente une « explosion combinatoire » ; c’est à dire lorsque le nombre de solutions augmente de manière combinatoire à mesure que la taille du problème augmente. Par exemple, il faudrait énumérer 60 solutions afin de résoudre le problème du voyageur de commerce pour six villes et plus de 4.10³º solutions pour trente villes² ! La figure suivante décrit ce phénomène.
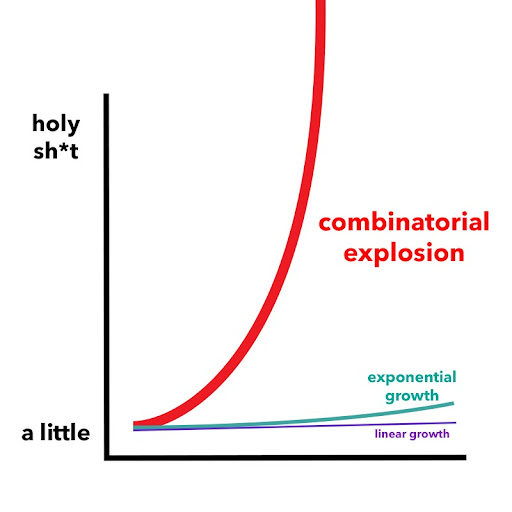
Cet article n’a pas pour vocation de lister toutes les méthodes d’optimisation combinatoire³ de manière exhaustive. Néanmoins, on distingue par exemple des méthodes dites « exactes » comme la programmation linéaire en nombres entiers (PLNE) et des méthodes dites « approchées » à base d’heuristique. Les premières garantissent d’atteindre une solution optimale mais le temps d’exécution peut s’avérer prohibitif alors que les secondes permettent d’obtenir des solutions admissibles souvent sans garantie d’atteindre l’optimum tout en réduisant la complexité algorithmique. Choisir a priori une approche ou l’autre n’est pas forcément souhaitable et ce choix dépend essentiellement du problème à résoudre et de la taille de l’instance à traiter. En tout état de cause, une approche exacte de type MIP est intéressante à tester de prime abord. Mais si l’exécution prend trop de temps, arrêter la résolution du MIP avant la résolution complète est aussi un moyen d’obtenir une solution approchée. Sinon, d’autres méthodes approchées sont à tester, qui s’exécutent très rapidement avec des solutions d’excellente qualité et proches de l’optimum.
Les solutions d’optimisation trouvent par exemple toute leur valeur dans les fonctions Achats des entreprises. En effet, dans de nombreuses sociétés, les services d’achat sont régulièrement confrontés à un problème d’optimisation spécifique : à quel fournisseur faut-il allouer ma demande de manière optimale ? Autrement dit, ce problème sert à allouer chaque demande d’achat au meilleur fournisseur. Ce problème d’allocation (ou assignment) ne vise pas uniquement à minimiser le coût total des achats mais il doit également respecter un certain nombre de contraintes métiers, comme :
Le non-respect de ces contraintes peut causer des pénalités financières significatives.
Prenons le cas de 250 demandes à allouer à 4 fournisseurs avec les contraintes de parts de marché incluant pénalités et des réductions de prix selon certaines quantités de produits achetés. Une première méthode approchée dite glouton a été employée pour allouer incrémentalement chaque demande au fournisseur le moins cher, avec une durée d’exécution inférieure à 1 seconde ; autrement dit, cette approche affecte le fournisseur avec le prix (réduit ou non) le plus bas demande après demande. La seconde méthode exacte de type MILP a été lancée pendant 1.2 secondes et la solution obtenue présente l’intérêt de respecter plus de parts de marché et réduire le coût global de presque 50% par rapport à la solution du glouton. La figure suivante illustre ce cas d’étude :

Il existe une communauté active francophone fédérée autour de la société ROADEF (Société française de recherche opérationnelle et d’aide à la décision), créée en 1998. La ROADEF organise chaque année un congrès réunissant la communauté française de recherche opérationnelle, et l’association met en ligne de nombreux contenus (livres, liens, annonces, forums, actus, formations) sur son site.
______________________________________________________
¹ L’optimisation vise à répondre à des problèmes de décision ou d’affectation (prescriptif) alors que les autres branches de l’IA interviennent souvent plus en amont (source).
² Pour le problème du voyageur de commerce, le nombre de solutions est de (n-1)!/2, où n est le nombre de villes à visiter
³ Une hiérarchisation des techniques d’optimisation est notamment disponible ici.
______________________________________________________
Vous avez une idée de cas d’utilisation impliquant de l’optimisation combinatoire mais vous faites face à une explosion combinatoire ?
Contactez-nous pour identifier dans quelle mesure la R.O. pourrait vous être utile.
Lorem ipsum dolor sit amet consectetur. Ipsum penatibus viverra feugiat amet varius pharetra porta risus lectus. Turpis enim massa non tincidunt in faucibus.

